Introduction

Knowledge of the three-dimensional structure is a prerequisite for the rational design of site-directed mutations in a protein and can be of great importance for the design of drugs. Structural information often greatly enhances our understanding of how proteins function and how they interact with each other or it can, for example, explain antigenic behaviour, DNA binding specificity, etc. X-ray crystallography and NMR spectroscopy are the only ways to obtain detailed structural information. Unfortunately, these techniques involve elaborate technical procedures and many proteins fail to crystallize at all and/or cannot be obtained or dissolved in large enough quantities for NMR measurements. The size of the protein is also a limiting factor for NMR.

In the absence of experimental data, model-building on the basis of the known three dimensional structure of a homologous protein is at present the only reliable method to obtain structural information [1-26]. Comparisons of the tertiary structures of homologous proteins have shown that three-dimensional structures have been better conserved during evolution than protein primary structures [27-45,65], and massive analysis of databases holding results of these three dimensional comparison methods [46-49], as well as a large number of well studied examples [e.g. 50-58] indicate the feasibility of model-building by homology.

All structure prediction techniques depend one way or another on experimental data. This is most easily seen for model building by homology, but also secondary structure prediction programs are trained on proteins with a known three dimensional structure, and even molecular dynamics force fields are mainly derived from protein and peptide data. Unfortunately, all protein structures contain errors [61]. Hence, verification of the data used in modeling procedures is a prerequisit for good results [59-64,80,81]. Many of the same verification techniques can of course also be used to get an impression of the quality of the model.

Model building by homology is a multi step process. At almost all steps choices have to be made. The modeller can virtually never be sure that she makes the best choices, and thus a large part of the modelling process consists of serious thought about how to gamble between multiple seemingly similar choices. As this process resembles very strongly what goes on in the mind of a professional gambler who visits the Loutrakis cassino, some introduction in game theory seems in place.

Professional gambling, the game of 21

It is commonly believed that the developement of the theory of probabilities started when Fermat and Pascal in the 17-th century worked out the optimal strategy for certain popular gambling games. One does not need much imagination to see a (still) rich nobleman loosing game after game at the card or crap table coming up with the idea to pay somebody really smart, i.e. Fermat or Pascal, to work out a winning strategy for him.

Upon playing the game of 21 in a casino the objective of both the player and the house is to get cards the face values of which add up to as closes as possible to 21, but not over 21. If this were all the rules, both players would have a 50% chance of winning, and the casino would go bankrupt rather soon. Casinos therefore add many rules, the worst one for the player being that upon equal points the house wins. A player who can remember all the cards that were taken of the pile till the moment the decission wether to ask for one more card or not has to be made has much better chances of winning than somebody who assumes that every of the 52 possible cards always has a chance of 1/52 of being the next one on top of the pile. Normally around eight packs of 52 cards are combined and randomly shuffled to make it more difficult to remember all the already used cards, and to ensure that the chances donıt deviate too much from 1/52 shortly after a new pile of cards is introduced. Although many casinos use different house-rules for the game 21, on average the chance of the house beating a player who remembers all the cards and plays optimally is better than 50% till about 1/2 till 3/4 of all cards of the pile have been used. And when that fraction of the cards has been used, the not yet used cards normally are discarded and a new pile of cards is introduced.

So, how should one proceed to have the best chances of winning? Formula 1 describes how the dollars earned, or the profit (D$), depend on the external parameters:

	D$ = E(Rounds) * F(Table) * N(card1,card2, ... cardK)    /1/

	ln(D$)=R*T*ln(N(cardK))	                                 /2/

	DG = RTln(K)                                             /3/

What makes the game of 21 so important for homology modelling? Well, upon building a model by homology very often decissions have to be made which essentially boil down to gambling. If the side chain of a residue has to be placed one often has to select between several seemingly good rotamers. At such moments, one should not assume that if there are N rotamers to choose from, each with a 1/N chance of being correct, but rather one should try to obtain as much information as possible to obtain the real probabilities, and select the most probable rotamer. The 21 player can use `theoretical` information, such as the cards already taken from the pile, the card on the bottom of the pile if he were smart enough to look at that one when the opportunity was there, and more experimental data such as the shape of the coffee stain left on the card at a previous occasion. The homology modeller can use theoretical information such as rules obtained from from database searches, multiple sequence alignments, multiple homologous structures, quantum chemical calculations, and more experimental information such as the results of mutagenesis or ligand binding studies, etc. What they have in common is that all sources of information, if treated with proper statistical rigour, will improve the chance that the final outcome is optimal. In the next paragraph the subsequent steps to be taken when modelling a protein by homology will be described. In subsequent paragraphs these steps will be elaborated upon, and the hints that the professional gambler can give the modeller will be listed.

Modeling overview

Differences between three-dimensional structures increase with decreasing sequence identity and accordingly the accuracy of models built by homology decreases [1,2].

The errors in a model built on the basis of a structure with >90% sequence identity may be as low as the errors in crystallographically determined structures, except for a few individual side chains [1,62]. If, as a test case, a known structure is built from another known structure, then in case of 50% sequence identity the RMS error in the modeled coordinates can be as large as 1.5 Angstrom, with considerably larger local errors. If the sequence identity is only around 25% the alignment is the main bottleneck for model building by homology, and large errors are often observed. With less than 25% sequence identity the homology often remains undetected. In figure 1 the key limiting factors in modeling as a function of sequence identity are shown.

At present most model building by homology protocols start from the assumption that, except for the insertions and deletions, the backbone of the model is identical to the backbone of the structure. In practice, however, domain motions and 'bending' of parts of molecules with respect to each other is often seen. Even in case of significant bending short range interactions will not differ very much and the model will be perfectly adequate for rational protein engineering, etc. However, the prediction of local differences in the backbone between structures that are homologous in sequence still requires much research, some aspects of which will be described below.

In recent years automatic model-building by homology has become a routine technique that is implemented in most molecular graphics software packages. Currently the emphasis in literature is on a few topics:

• Improvement of the way side chains are positioned in the modelled structure, and improvement of the energetics or database techniques needed to do this fast and accurate.
• Development of techniques to check the quality of models.
• Improvement of the sequence alignment that is at the basis of the model-building procedure, and evaluation of the significance of alignments.
• Development of secondary structure prediction and ab initio 3D modeling techniques.

The modelling process

The modelling process can be subdivided into 9 stages:

• template recognition;
• alignment;
• alignment correction;
• backbone generation;
• generation of canonical loops (data based);
• side chain generation plus optimisation;
• ab initio loop building (energy based);
• overall model optimisation (energy minimisation);
• model verification with optional repeat of previous steps.

What can be modelled?

As will be described described below, the transfer of structural information to a potentially homologous protein is straightforward if the sequence similarity is high, but the assessment of the structural significance of sequence similarity can be difficult when sequence similarity is low or restricted to a short region.

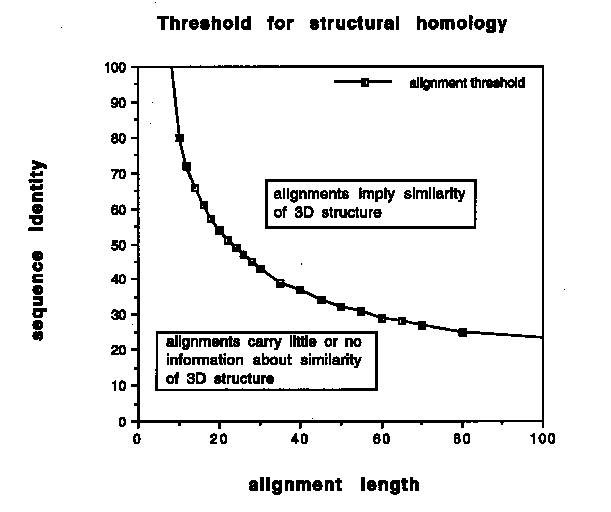
Figure 2. Homology threshold for structurally reliable alignments as a function of alignment length [free after 2].

The homology threshold (curved line) divides the graph into a region of safe structural homology where essentially all fragment pairs are observed to have good structural similarity and a region of homology unknown or unlikely where fragment pairs can be structurally similar but often are not, without a chance of predicting what it will be. At present 15% of the known protein sequences fall in the safe area, which implies that 15% of all sequences can be modelled and thus are open to structure function relation studies.

This indicates a key problem: the shorter the length of the alignment, the higher the level of similarity required for structural significance. Chothia and Lesk [1] have studied the relation between the similarity in sequence and three-dimensional structure for the cores of globular proteins. To quantify this problem, Schneider and Sander [2] calibrated the length dependence of structural significance of sequence similarity. This was done by deriving from the database of known structures a quantitative description of the relationship between sequence similarity, structural similarity and alignment length. The resulting definition of a length-dependent homology threshold (see figure 2) provides the basis for reliably deducing the likely structure of globular proteins down to the size of domains and fragments.

Template recognition

If the percentage sequence identity between the sequence of interest and a protein with known structure is high enough (more than 25 or 30 %) simple database search programs like FASTA [78] or BLAST [79] are clearly adequate to detect the homology. If, however, the percentage identity falls below 25% detection by straigthforward sequence alignment becomes problematic, and more advanced techniques are required. One technique that is currently being worked on is threading. This topic will be discussed further down in this review.

Alignment

In a 'normal' sequence alignment one puts both sequences along the axes of a big matrix. The matrix elements are filled with numbers indicating the likelyhood that the two corresponding amino acids aught to be aligned. These probabilities are normally obtained from a scorings, or exchange matrix which holds values for the 380 possible mutations and the 20 identities; these matrices normally are symmetric. Figure 3 shows an example of an exchange matrix. It is clearly seen that the values on the diagonal, representing conserved residues, are highest, but one can also observe that exchanges between residue types with similar physico chemical properties get a better score than exchanges between residue types that wildely differ in their properties.

The alignment process simply consists of finding the best path through this matrix. The best path is found by taking the little yellow eater from the famous video game Œpack-manı and letting it start near the top left corner and eat its way to somewhere near the lower right corner.

   A  C  D  E  F  G  H  I  K  L  M  N  P  Q  R  S  T  V  W  Y		Figure 3.
A  5 -2  0  1 -2  0  0 -1  0 -1  0  0  1  0 -1  1  0  0 -2 -2  		Example of an
C -2  8 -2 -3 -3 -2  0 -2 -3 -3  0 -2 -3 -3 -2 -1 -1 -2 -1 -2  		exchange or
D  0 -2  5  2 -2  0  1 -3  0 -2 -1  2  0  1 -2  0  0 -2 -3 -2  		scorings matrix.
E  1 -3  2  5 -3  0 -1 -2  1 -2 -2  1  1  2  0  1  1 -1 -2 -1  
F -2 -3 -2 -3  6 -3  1  0 -3  2  2 -3 -2 -3 -2 -1 -2  0  3  3  
G  0 -2  0  0 -3  5 -1 -2  0 -2 -2  0  0 -1  0  0 -1 -1 -2 -3  
H  0  0  1 -1  1 -1  5 -1  1 -1  0  1  0  1  2  0  1 -1  0  1  
I -1 -2 -3 -2  0 -2 -1  5 -2  2  2 -2 -2 -3 -2 -1  0  2  0  0  
K  0 -3  0  1 -3  0  1 -2  5 -1 -2  1  0  1  2  0  0 -1 -2 -2  
L -1 -3 -2 -2  2 -2 -1  2 -1  5  3 -2 -2  0 -1 -1  0  2  0  0  
M  0  0 -1 -2  2 -2  0  2 -2  3  5 -1 -2  0 -2 -1  0  1 -2 -1  
N  0 -2  2  1 -3  0  1 -2  1 -2 -1  5 -2  1  0  2  0 -2 -3 -1  
P  1 -3  0  1 -2  0  0 -2  0 -2 -2 -2  8  0  0  0  0 -1 -3 -3  
Q  0 -3  1  2 -3 -1  1 -3  1  0  0  1  0  5  2  1  0 -1 -1 -2  
R -1 -2 -2  0 -2  0  2 -2  2 -1 -2  0  0  2  5  1  0 -1  0 -1  
S  1 -1  0  1 -1  0  0 -1  0 -1 -1  2  0  1  1  5  2 -1  0  0  
T  0 -1  0  1 -2 -1  1  0  0  0  0  0  0  0  0  2  5  0 -1 -2  
V  0 -2 -2 -1  0 -1 -1  2 -1  2  1 -2 -1 -1 -1 -1  0  5 -1  0  
W -2 -1 -3 -2  3 -2  0  0 -2  0 -2 -3 -3 -1  0  0 -1 -1  6  3  
Y -2 -2 -2 -1  3 -3  1  0 -2  0 -1 -1 -3 -2 -1  0 -2  0  3  6  

	ASTPERASWLGTA  and  VATTPDKSWLTV.

		 V  A  T  T  P  D  K  S  W  L  T  V	   Figure 4.
	A	 0  5  0  0  1  0  0  1 -2 -1  0  0	   The alignment
	S	-1  1  2  2  0  0  0  5  0 -1  2 -1	   matrix for
	T	 0  0  5  5  0  0  0  2 -1  0  5  0	   two sequences.
	P	-1  1  0  0  8  0  0  0 -3 -2  0 -1	   Scores obtained
	E	-2  1  1  1  1  2  1  1 -2 -2  1 -1	   from figure 3.
	R	-1 -1  0  0  0 -2  2  1  0 -1  0 -1
	A	 0  5  0  0  1  0  0  1 -2 -1  0  0
	S	-1  1  2  2  0  0  0  5  0 -1  2 -1
	W	-1 -2 -1 -1 -3 -3 -2  0  6  0 -1 -1
	L	 2 -1  0  0 -2 -2 -1 -1  0  5  0  2
	G	-1  0 -1 -1  0  0  0  0 -2 -2 -1 -1
	T	 0  0  5  5  0  0  0  2 -1  0  5  0
	A	 0  5  0  0  1  0  0  1 -2 -1  0  0

Obviously, the path should at every step go at least one line down, and at least one column to the right. The best path is indicated by the characters in bold, but why is the underlined alternative near the lower right corner not better? After all, it Œeatsı more points? Well, alignment of sequences is not entirely a video game, but an attempt to capture evolutionary events in numbers. Comparing thousands of sequences and sequence families it became clear that exchanges have a chance of ocurring inversly proportional to the numbers in figure 3, but deletions, like the one indicated by underlining in figure 4 are about as unlikely as at least a couple of non-identical residues in a row. The jump roughly in the middle in the bold face character on the other hand is genuine because after the jump we earn lots of points (5,6,5) which without the jump would have been (1,0,0). Making the right decission about gaps is a whole independent line of research, and this short summary definitely does not give sufficient credits to the scientists working on this problem. But, as shown in the next paragraph, for the homology modeller it is not so very much important to get the gaps right immediately because she can often improve the location of deletions or insertions after building the first model. Just like the 21 player improves his chances a lot if he were allowed to try again with another last card after he went bust, the modeller improves her changes a lot by analysing the original structure and the model, and iteratively adapting the alignment based on the evaluation of the model.

Improving the alignment using multiple sequences

The alignment process described above is clearly open for improvements. The professional gambler will definitely not like the idea that every similar exchange, for example from alanine to glutamic acid, always has the same score, or in other words, the same chance of occurring. In the three dimensional structure of the protein it is surely not likely to see an Ala->Glu mutation in the core, but at the surface this mutation is as likely as every other one. There are two ways to address this problem. One is the use of multiple sequence alignments, often based on profiles [82-90], and the other is called threading [66-77] (unfortunately too often still pronounced: shredding).

The use of multiple sequence alignment methods for the alignment of only two sequences is based on an idea that our professional gambler would not like very much, namely that if something is observed very often, it is probably more likely to occur. Although there is no physical reason to base this assumption on, common sence and practical experience support it strongly. So, rather than aligning just the sequence of interest and the sequence of the template structure, all sequences that are member of this same family are aligned. In such a multi sequence alignment one normally puts higher weights on residue positions where little variation is observed, and tries to get deletions only in areas where the sequences are strongly divergent.

One of the major advantages of the use of multiple sequences can be explained by the following hypothetical (pathological) sequence alignment problem:

Suppose you want to align the sequence LTLTLTLT with YAYAYAYAY. There are two equally poor possibilities:

LTLTLTLT     or     LTLTLTLT					Figure 5. Pathological
YAYAYAYAY          YAYAYAYAY					alignment problem.

  LTLTLTLT							Figure 6. Solution for
 TYTYTYTYT							the pathological
  YAYAYAYAY							alignment problem.

Improving the alignment using the model

Threading methods in general incorporate knowledge extracted from the structure of the template, and try to improve the sequence alignment using this information. The aforementioned Ala->Glu mutation would, for example, at the surface get a score of 2 on the scale of figure 3, but in the core of the protein the score would become -5. A good threading program incorporates such, and many more similar considerations. The idea is really simple, and therefore must be brilliant. In practice however, most threading methods are reasonably successful in detecting templates, but strangely enough, when it boils down to the nitty gritty details of the actual alignment, they fail hopelesly [72]. Nevertheless, most modellers use this method manually. If, in the model, a buried glutamic acid is observed the first reaction is to see which alternative alignment would put this negatively charged residue at the surface of the model.