Pairwise Alignments

Dotplot analysis

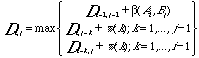
A direct way of comparing sequences is the dotplot analysis. The two sequences to be compared form the rows and columns of a matrix, and in the simplest case a dot is plotted in a graphical representation of the matrix wherever the sequences are identical. In practice, the comparison is most often done in a window of specified length, and a dot is put in the graph whenever the score within this window is above a certain specified threshold. The score might be calculated as the number of identities or as a similarity based on a scoring matrix. Sequence similarities will be obvious as diagonals in the plot. The method does not align sequences but it is a quick way of spotting similarities. It has the additional advantage over other alignment methods that it can detect repetitions (parallel diagonals) and permutations in the sequences.

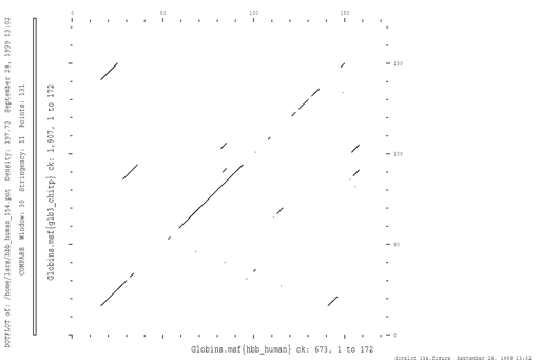
A dotplot analysis of the sequences of human hemoglobin a chain and Erythrocruorin from Chironomus.

Dotplots are useful to visualize potential similarities between proteins, however they are not really useful for large scale comparisons as they need manual inspection.

Global Alignment (Needleman-Wunch)

Global alignments aim at optimally aligning two or more sequences. The most used methods for global alignments are based on algorithms originally developed by Needleman and Wunch and modified by Sellers . This procedure (the NWS method) is using a dynamic programming algorithm that simplifies the enormous task of calculate a score for all possible alignments of two sequences with gaps of any lengths. The sequences to be aligned are arranged as rows and columns of a rectangular matrix. A score is calculated for each position of the matrix according to three possible events: replacement (or conservation) of a residue, insertion in sequence A or insertion in sequence B. The matrix elements D_i,j are filled with numbers according the rule.

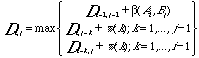
Here the first alternative corresponds to the case of no insertions or deletions: to the previous diagonal element is added the score b for the current pair of residues (A_i, Bj). The other two alternatives correspond to insertions in A or B: to the element above or to the left is added the score for a deletion of length k. The scoring begins at the first element of the matrix, corresponding to one end of the sequences. An example using a short nucleotide sequence is shown in the figure below. The total score is found as the last element in the matrix. The actual sequence alignment is obtained from the path through which this numbers is obtained.

Alignment of two nucleotide sequences. Here a match has a score of +3, a mismatch a score of -1. Gaps are scored by -3 for insertion of a gap and -1 for each inserted residue (w=-3-k). The scores are calculated from the 5' end. Bold numbers show the path for reaching the highest number.

The obtained alignment looks like this:

GCCAA-GTAGG-
ACGAGCGTATGA
    

So how was this matrix obtained ? To symbolize this we write all the D values for the first four nucleotides:

At one position of this example, the alignment is ambiguous. In this particular case, it is the trivial difference of where to put the single gap in the top sequence. It is important to note that any sequences can be aligned using these procedures, irrespective of their possible homology. The standard implementation of the DP algorithm present one solution and do not show alternative alignments with the same score.

Ends free global alignment

In a global alignment, gaps at the beginning and end of the sequences have the same gap penalties as gaps in other parts of the sequences. This has the effect that the algorithm will try to align all of the two sequences. If the sequences are of different lengths or if only parts of the sequences are similar this might have negative effects. One way to handle such cases is not to penalize gaps at the ends of the sequences. The figure below shows the same sequences aligned under this condition. The optimal alignment is chosen as the one giving the highest number in the last row or column. In this case, the alignment of the same nucleotide sequence is different, but the same number of identities has been obtained.

Alignment with no gap penalty at ends (first row and column initiated with 0), using the same scoring parameters. The alignment is different from that of the table above.

Obtained alignment

----GCCAAGTAGG-
ACGAGC---GTATGA

Local alignments (The Smith-Waterman algorithm)

The dynamic programming algorithm can also be used for finding local sequence similarities. The Smith and Waterman algorithm is very similar to the NWS method except that a calculated negative number for a matrix position is replaced by zero, indicating that no sequence similarity has been detected up to that point. When all the matrix element have been calculated, the maximum number in the matrix is located, and the alignment is traced back from this point until the first positive number. The same sequences as above aligned with these assumptions are shown in Fig. xii. Once more, a different alignment is obtained with the simple test sequence. Only the aligned parts of the sequences are shown as output of this procedure.

Fig. Xii. Local alignment with no negatives. The alignment is different from the above examples and corresponds only to the positive numbers in the matrix ending up with the maximum number.

 
-CAAG--TAGG- 
-CGAGCGTATG-

It is of course also possible to use local alignments for protein sequences as exemplified below:

Fig Xiii shows the alignment of two short segments of protein sequence. A segment of six amino acids give a total maximum score of 15 using the BLOSUM62 matrix and is presented as the output of the local alignment.

Alignment

VDNTAH
IDQTVN